How to Solve Limits: A Comprehensive Guide

Limits are a fundamental concept in calculus that help us determine the value a function approaches as the input gets closer to a particular point. There are various methods to evaluate limits, and in this blog, we will explore some of the most effective techniques. Solve Limits

Understanding toSolve Limits

Solve Limits Sometimes, directly substituting a value into a function results in an undefined expression such as 0/0 or infinity/infinity. In such cases, we need alternative methods to evaluate the limit. These include:

1. Direct Substitution
2. Factoring
3. Rationalizing the Numerator
4. Finding the Lowest Common Denominator
5. L’Hôpital’s Rule
6. Limits at Infinity and Rational Functions

Let’s explore each method in detail.

1. Direct Substitution

For functions that are continuous at a given point, the easiest way to evaluate the limit is by directly substituting the value of x.

Example:

If substitution results in a valid number, then that is the limit. However, if it gives an indeterminate form (e.g., 0/0), we need to use other methods.

2. Factoring

Factoring can simplify expressions where direct substitution results in 0/0. By factoring and canceling out common terms, we can find the limit.

Example:

Factorizing the numerator: Cancel (x – 1):

3. Rationalizing the Numerator

For limits involving square roots, multiplying by the conjugate can help simplify the expression.

Example:

Multiply numerator and denominator by the conjugate : This simplifies to: Cancel (4 – x): Substituting x = 4:

4. Finding the Lowest Common Denominator

When dealing with complex rational functions, finding the lowest common denominator (LCD) helps simplify the expression before evaluating the limit.

Example:

Finding the LCD for the numerator: Thus, the given function simplifies to: Now, substituting x = 0 gives -1/36 as the limit.

5. L’Hôpital’s Rule

When substitution results in indeterminate forms (0/0 or infinity/infinity), we can use L’Hôpital’s Rule, which involves differentiating the numerator and denominator separately and then evaluating the limit.

Example:

Differentiate the numerator and denominator: Now, evaluating the new function:

6. Limits at Infinity and Rational Functions

For rational functions, the limit as x approaches infinity depends on the degrees of the numerator and denominator:

• If the numerator’s degree is less than the denominator’s degree, the limit is 0.
• If the numerator’s degree is equal to the denominator’s degree, the limit is the ratio of leading coefficients.
• If the numerator’s degree is greater than the denominator’s degree, the limit is infinity or does not exist.

Example:

Since the degree of the numerator (3) is greater than that of the denominator (2), the limit approaches infinity.

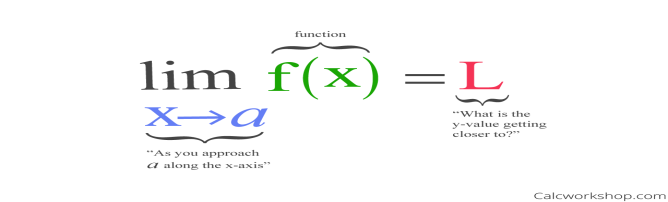
Conclusion

Solving limits requires different techniques depending on the function. Start with direct substitution, and if it leads to an indeterminate form, try factoring, rationalizing, or using L’Hôpital’s Rule. Understanding these techniques will make evaluating limits easier and more intuitive. Keep practicing, and mastering limits will become second nature!