Introduction
Solving Proportion Problems are a fundamental mathematical concept that links ratios and fractions to everyday situations, such as adjusting recipes, interpreting maps, and scaling models. In this guide, we will explain what a proportion is, why it matters, and provide simple steps to solve proportion problems effectively.
What Are Proportions?
Solving Proportion Problems is a mathematical statement that two ratios are equal. It is expressed in the form:
Examples of Proportions:
a/b = c/d
x/5 = 2/10
Proportions are essential for comparing quantities and have wide applications in mathematics, science, and real-life scenarios, such as resizing images or designing buildings.
Applications of Proportions:
Real-World Uses: Adjusting recipes, reading maps, and creating scale models.
Mathematics: Solving algebraic equations and understanding geometric concepts.
Science: Unit conversions and calculating concentrations.
Types of Proportions
Direct Proportion: When one value increases, the other increases as well.
Example: The distance traveled is proportional to the time when moving at a constant speed.
Inverse Proportion: When one value increases, the other decreases.
Example: The relationship between speed and travel time for a fixed distance.
Step-by-Step Guide to Solving Proportions
Identify the two ratios in the problem and ensure the units are consistent.
Example:
If 3 pencils cost $6, how much will 5 pencils cost?
Given ratios: 3/6 = x/5
Step 2: Set Up the Proportion
Write the given ratios as fractions and set them equal to each other:
3/6 = x/5
Step 3: Solve Using Cross-Multiplication
Multiply across the diagonal:
a × d = b × c
For our example:
3 × x = 6 × 5
3x = 30
Step 4: Isolate the Variable
Divide both sides by the coefficient of x:
x = 30 ÷ 3 = 10
Thus, 5 pencils cost $10.
Visualizing Proportions with Graphs
Graph 1: Direct Proportion
To graph a direct proportion:
Create a table of values.
Example: For y = 2x
x y
1 2
2 4
3 6
Connect the points with a straight line passing through the origin.
Graph 2: Inverse Proportion
To plot an inverse proportion like y = 10/x:
Create a table of values:
x y
1 10
2 5
5 2
Common Mistakes to Avoid
Incorrect Cross-Multiplication – Ensure calculations are performed correctly.
Ignoring Unit Consistency – Keep the same units across ratios.
Misinterpreting the Problem – Clearly identify direct or inverse proportion.
Practice Problems
If 4 apples cost $8, how much will 10 apples cost?
4/8 = 10/x
8 × 10 = 4 × x
80 = 4x
x = 80 ÷ 4 = 20
Answer: 10 apples cost $20.
A car travels 150 km in 3 hours. How far will it travel in 5 hours?
150/3 = x/5
150 × 5 = 3 × x
750 = 3x
x = 750 ÷ 3 = 250
Answer: The car will travel 250 km in 5 hours.
If y is directly proportional to x, and y = 12 when x = 4, find y when x = 10.
y = kx
12 = 4k
k = 12 ÷ 4 = 3
y = 3 × 10
y = 30
Answer: When x = 10, y = 30.
Advanced Applications of Proportions
Solving Geometry Problems: Used in similar triangles and shape scaling.
Calculating Scale Factors: Helps in map reading and model construction.
Data Analysis: Proportions are widely used in statistics and business calculations.
For Example:
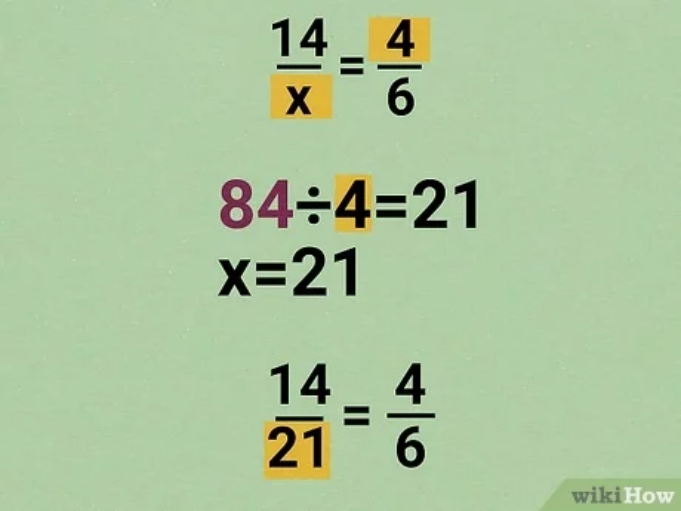
Conclusion
Proportions are a valuable mathematical tool with numerous real-world applications. By following a step-by-step approach and using visual aids like graphs, you can effectively solve proportion problems and apply them in practical situations.

