How to Solve a Piecewise Function: A Comprehensive Guide
Piecewise Function might seem intimidating at first, but once you understand them, they become a fascinating and versatile tool in mathematics. These functions allow you to model real-world scenarios where behavior changes under different conditions. In simple terms, a piecewise function is defined by different rules or formulas for specific intervals or conditions. This makes them incredibly useful for solving problems that can’t be represented by a single, straightforward formula.

For example, piecewise functions are commonly used in calculating tax brackets, where the tax rate changes depending on your income range. They’re also used in determining shipping costs, where the rate varies based on the weight of the package or the destination. By breaking down these problems into smaller, more manageable pieces, piecewise functions provide a flexible way to represent complex situations.
You’ll encounter piecewise functions in everyday life, from utility pricing to calculating overtime pay for workers with varying hourly rates. Learning how to work with them opens up a world of practical applications, from solving engineering problems to analyzing business revenue models.
What Are Piecewise Functions?
A piecewise function is a function defined by multiple sub-functions, each of which applies to a specific interval. The domain of the function is divided into different parts, and each part has its own formula or rule. Think of it like a puzzle: each piece fits only in its designated place.
To solve a piecewise function, you first need to identify the formula or rule that applies to each interval. The behavior of the function changes depending on the conditions for each interval. For instance, the function might behave differently for negative inputs compared to positive inputs. Understanding these rules is crucial for applying the correct formula to the correct interval.
In real-world scenarios, piecewise functions are used in modeling pricing tiers, speed limits in different zones, and more. They allow us to create functions that adapt to specific conditions, providing precise solutions for different parts of a problem.
How Do Piecewise Functions Work?
A piecewise function behaves differently based on the input value. It’s defined in intervals, and each interval has its own formula. For example, if the input falls into a specific range, you’ll use the corresponding formula for that range. These formulas can be as simple as a straight line or as complex as a parabola.
The key to solving piecewise functions is identifying the correct interval and applying the appropriate formula. Visualizing the function by graphing, it can also help you understand how it behaves across different intervals.
Graphing Piecewise Functions
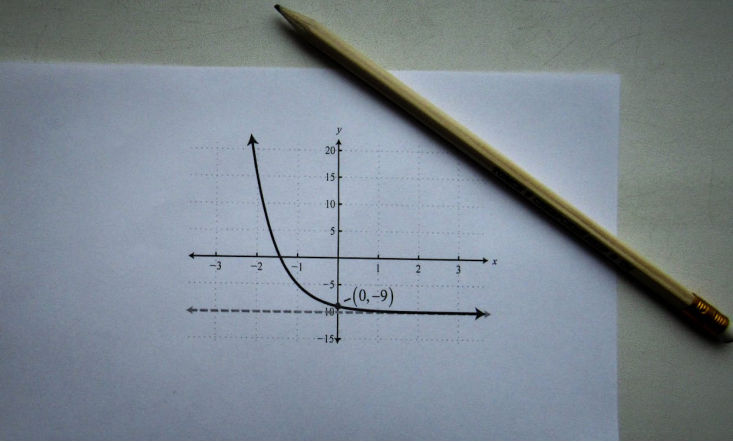
Graphing a piecewise function involves breaking it into smaller pieces, each defined by a specific formula over a certain interval. You plot each piece individually and then connect them based on the intervals.
Pay attention to the endpoints of the intervals:
Open dots indicate excluded endpoints (the function doesn’t include those points).
Closed dots indicate included endpoints (the function is defined at those points).
This helps you accurately represent the function’s behavior at the boundaries of each interval. Smooth transitions between pieces are essential for an accurate graph.
Evaluating Piecewise Functions
Evaluating a piecewise function involves a few simple steps:
1. Identify which interval the input falls into.
2. Apply the corresponding formula for that interval.
For example, if the input falls into the range defined by the first formula, plug the value into that formula to get the result. If it falls into the next interval, use the second formula.
The key is to ensure you’re using the correct formula for the correct interval. With practice, this process becomes second nature.
Continuity in Piecewise Functions
Continuity in piecewise functions refers to whether the function behaves smoothly without jumps or breaks. A function is continuous if the y-values align perfectly at the boundary points where different pieces meet.
To check continuity, examine the graph at the boundary points. If the y-values from the two pieces match, the function is continuous. If they don’t, there’s a discontinuity, meaning the function has a break in its graph.
Real-World Applications of Piecewise Functions
Piecewise functions are incredibly useful in real-world scenarios:
Tax Brackets: Different tax rates apply to different income ranges.
Shipping Costs: Rates vary based on weight or distance.
Utility Bills: Usage tires determine the rate (e.g., electricity or water).
Event Pricing: Different rates apply based on the number of attendees.
These examples show how piecewise functions simplify complex pricing structures by breaking them into manageable pieces.
Tips for Solving Piecewise Function Problems

1. Identify Intervals: Determine which interval the input falls into and use the corresponding formula.
2. Check Boundaries: Pay attention to whether endpoints are included (closed dots) or excluded (open dots).
3. Graph the Function: Visualizing the function helps you understand its behavior across intervals.
4. Focus on Continuity: Ensure smooth transitions between pieces to accurately represent the function.
Why Are Piecewise Functions Important?
Piecewise functions are essential for modeling real-world situations where behavior changes under different conditions. They allow us to break complex problems into smaller, more manageable pieces, making it easier to solve and understand them.
Their flexibility makes them ideal for modeling systems that don’t behave in a simple, linear way. Whether it’s electricity usage at different times of day or pricing changes in different market conditions, piecewise functions help create accurate and adaptable models.
Conclusion
Piecewise functions are a powerful tool in mathematics, enabling you to solve problems where the solution changes based on different conditions. Whether you’re working in algebra or calculus, mastering piecewise functions is a valuable skill.
By understanding how to evaluate, graph, and ensure continuity in piecewise functions, you’ll be well-equipped to tackle challenges in both academic and real-world applications. With practice, you’ll gain the confidence to solve a wide variety of piecewise function problems effectively
